Adversarial Example Generation
Adversarial Example Generation
皆さんは、AIモデルを作成する上で、セキュリティに関して考えたことはありますでしょうか??
実は入力画像に私たちが気づかないような摂動を加えるだけで、モデルの性能が大きく異なることがあります。
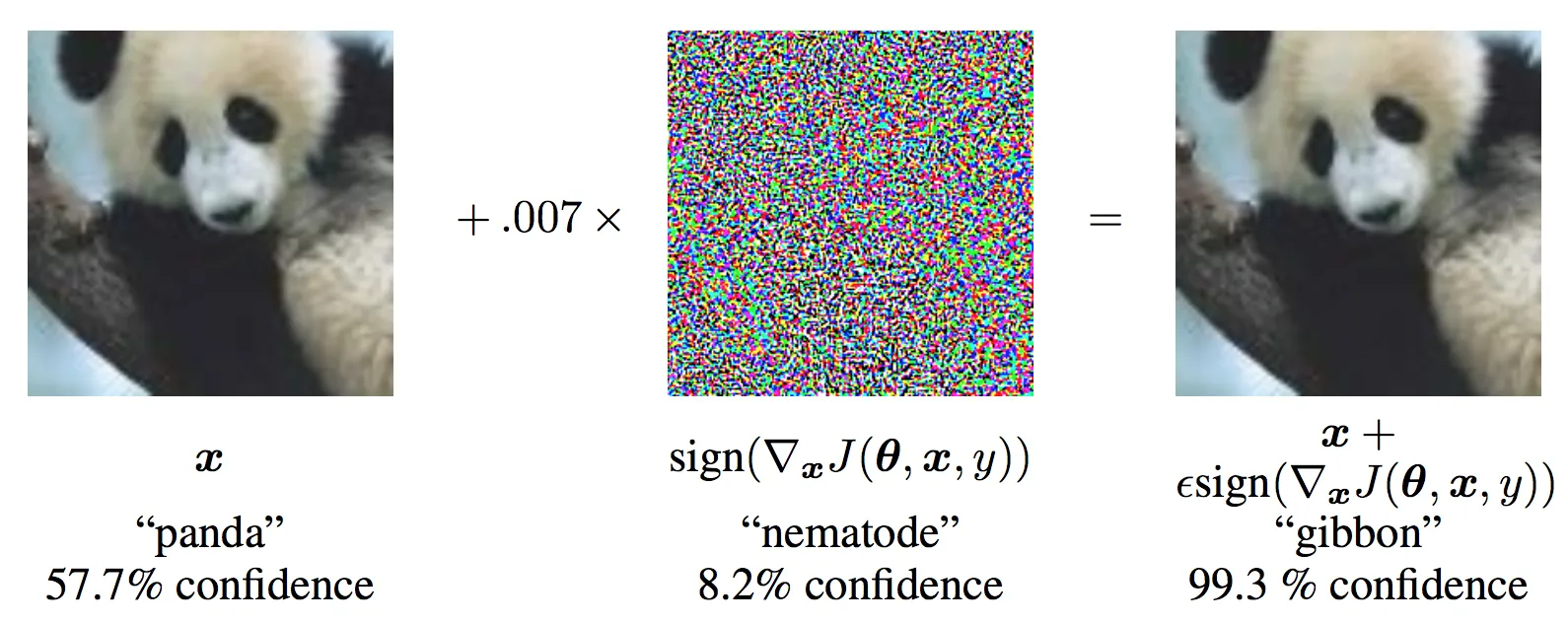
その例がまさに上記の画像になります。入力画像はどう見てもパンダなのですが、目に見えない摂動を加えるだけでテナガザルと判断するようになってしまいます(モデルは学習不足ではなく、十分に学習したもの)。
もし自分が作ったAIが、このような攻撃によって誤作動を起こし、周りの人たちに迷惑をかけたらなんて考えたら恐ろしいですよね...
今回の勉強会では、攻撃方法の一つであるFast Gradient Sign Method (FGSM) を使用してMNIST分類モデルを騙していきます!!
それではやっていきましょう!!!
1. Thread Model
敵対的攻撃には多くのカテゴリーが存在しており、それぞれ目的や攻撃者が持つ前提の知識が異なります。
一般的な目的は、入力データに最小限の摂動を加え、誤分類を引き起こすことになります。
また、攻撃する上での前提条件は大きく二つに分けることができ、以下のような攻撃が考えられます。
- ホワイトボックス攻撃 : アーキテクチャ、入力、出力、重みを含むモデルに関する情報を持ち、アクセスすることができる場合の攻撃
- ブラックボックス攻撃 : モデルの入力と出力のみにアクセスすることができ、アーキテクチャや重みについては何も知らない場合の攻撃
2. Fast Gradient Sign Method
Fast Gradient Sign Method (FGSM) は、最も有名な敵対的攻撃の一種であり、「GANの生みの親であるGoodfellow氏らが「Explaining and Harnessing Adversarial Examples」で述べています。これは、ニューラルネットワークの学習方法である勾配を利用して、ニューラルネットワークを攻撃するように設計されています。
モデルの学習というのは、逆伝搬された勾配に基づいて重みを更新し、損失値を最小化することで行われますが、そうではなく、損失値を最大化するように入力データを調整します。
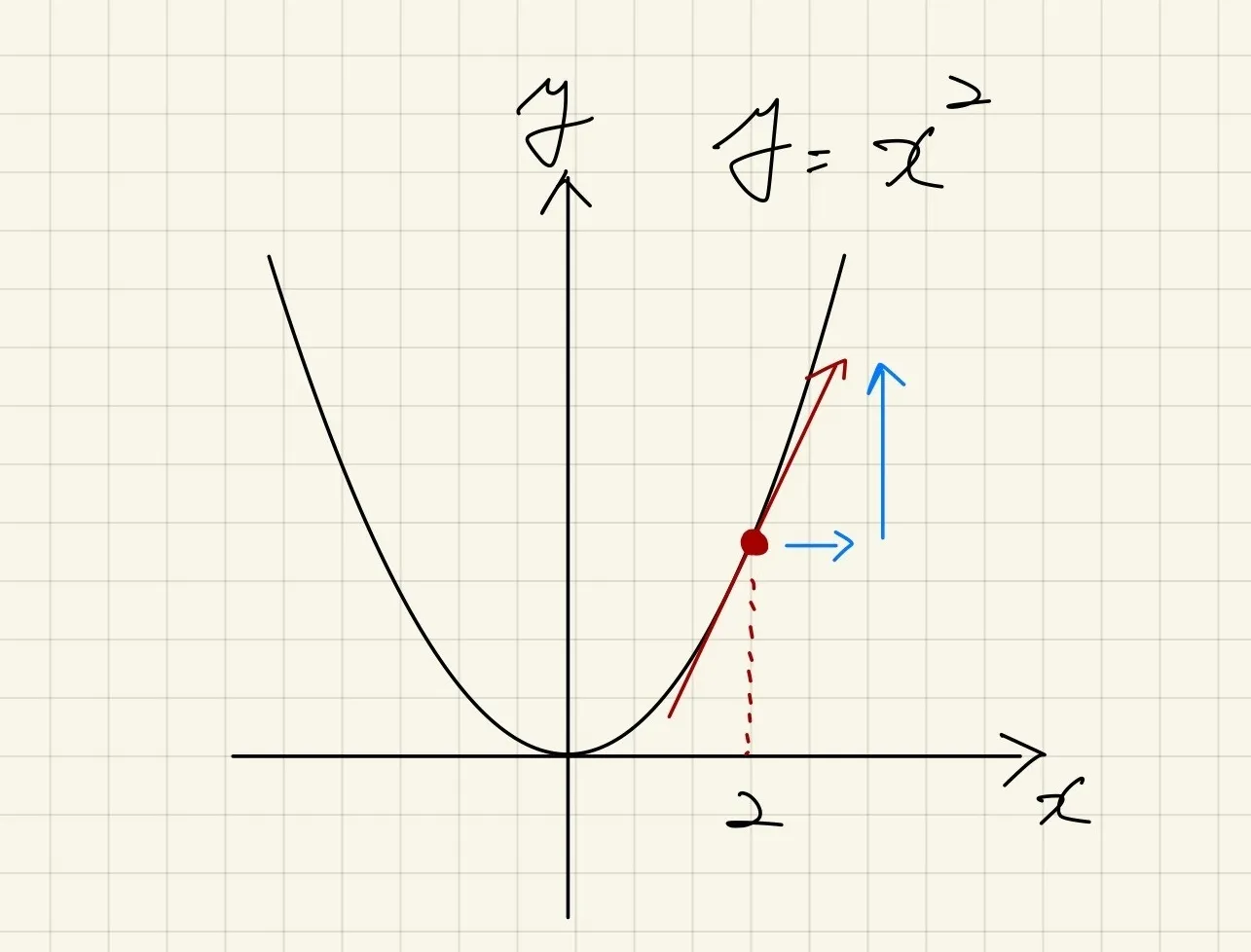
例えば、入力が
xで損失値がy=x2で与えられる場合、xに関する微分はy'=2xとなります。x=2の場合、勾配は4になります。損失値を小さくする場合、x=2を負の方向に更新すれば良いのですが、今回は大きくしたいので、正の方向に更新します。この考えをそのまま画像分類に適用します。

3. Code
MNISTの学習済みモデルの重みはこちら。
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import numpy as np
import matplotlib.pyplot as plt
# epsilonsによって攻撃の強さをコントロール
epsilons = [0, .05, .1, .15, .2, .25, .3]
# 学習済みMNIST分類モデルを使用
pretrained_model = "data/lenet_mnist_model.pth"
# GPUを使用
use_cuda=True
# seedを設定(同じ乱数が生成されるため再現できる)
torch.manual_seed(42)
今回使用するモデルを定義します。
# LeNet Model definition
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 32, 3, 1)
self.conv2 = nn.Conv2d(32, 64, 3, 1)
self.dropout1 = nn.Dropout(0.25)
self.dropout2 = nn.Dropout(0.5)
self.fc1 = nn.Linear(9216, 128)
self.fc2 = nn.Linear(128, 10)
def forward(self, x):
x = self.conv1(x)
x = F.relu(x)
x = self.conv2(x)
x = F.relu(x)
x = F.max_pool2d(x, 2)
x = self.dropout1(x)
x = torch.flatten(x, 1)
x = self.fc1(x)
x = F.relu(x)
x = self.dropout2(x)
x = self.fc2(x)
output = F.log_softmax(x, dim=1)
return output

学習済みのモデルを使用して、攻撃による影響を確認します。そのため、train_loaderではなく、test_loaderを作成します。datasets.MNISTを用いて、MNISTのテストデータを読み込みます。また、MNISTデータをtorch.Tensorに変換し、平均と標準偏差を用いて標準化します(MNISTはグレースケールなので、1チャネルしかありません)。ここでは一枚ずつ処理したいので、batch_sizeを1とします。
# MNIST Test dataset and dataloader declaration
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)),
])),
batch_size=1, shuffle=True)
deviceやmodelを定義し、推論のための準備をします。
# cudaが使える場合、deviceにcudaを、使えない場合はcpuを代入
print("CUDA Available: ",torch.cuda.is_available())
device = torch.device("cuda" if use_cuda and torch.cuda.is_available() else "cpu")
# モデルを定義し、deviceに渡す
model = Net().to(device)
# 定義したモデルに重みをロードする
model.load_state_dict(torch.load(pretrained_model, map_location=device))
# モデルをevaluationモードに(dropoutが不活性化する)
model.eval()
この勉強会のメインテーマである「FGSM Attack」を定義します。難しいことは全くなく、簡単に実装することができます。
# FGSM attack code
def fgsm_attack(image, epsilon, data_grad):
# 勾配に対してsign関数を適用(符号化)
sign_data_grad = data_grad.sign()
# 入力画像に対して上記で計算した摂動を加算
perturbed_image = image + epsilon*sign_data_grad
# 画像のレンジを整えるために[0,1]でclip
perturbed_image = torch.clamp(perturbed_image, 0, 1)
# Return the perturbed image
return perturbed_image
# restores the tensors to their original scale
def denorm(batch, mean=[0.1307], std=[0.3081]):
"""
Convert a batch of tensors to their original scale.
Args:
batch (torch.Tensor): Batch of normalized tensors.
mean (torch.Tensor or list): Mean used for normalization.
std (torch.Tensor or list): Standard deviation used for normalization.
Returns:
torch.Tensor: batch of tensors without normalization applied to them.
"""
if isinstance(mean, list):
mean = torch.tensor(mean).to(device)
if isinstance(std, list):
std = torch.tensor(std).to(device)
# 画像の形状に合わせて、標準化を行う
return batch * std.view(1, -1, 1, 1) + mean.view(1, -1, 1, 1)
最後にMNISTデータを用いてFGSM attackを行うコードを実装します。今回はイプシロンの値を変化させて、モデルに対する影響を確かめたいので、test関数を定義し、for文で回せるようにします。
def test( model, device, test_loader, epsilon ):
# Accuracy counter(予測と正解ラベルが一致した数を数える)
correct = 0
adv_examples = []
# 全てのMNISTのテストデータセットにおいて評価を行う
for data, target in test_loader:
# dataとtargetをdeviceに送る
data, target = data.to(device), target.to(device)
# FGSM attackでは入力データの勾配を計算する必要があるので、requires_gradをTrueにする
data.requires_grad = True
# モデルに入力し、出力を得る
output = model(data)
init_pred = output.max(1, keepdim=True)[1] # 10クラスの中で最大の確率のindexを取得
# 初期予測結果が間違っている場合、攻撃する必要がないので次の画像に移る
if init_pred.item() != target.item():
continue
# 正解の場合、損失値を計算
loss = F.nll_loss(output, target)
# モデルの勾配をゼロに
model.zero_grad()
# 逆伝播により勾配を計算
loss.backward()
# 入力データに対する勾配を取得
data_grad = data.grad.data
# Restore the data to its original scale
data_denorm = denorm(data)
# FGSM attackを行う
perturbed_data = fgsm_attack(data_denorm, epsilon, data_grad)
# もう一度標準化
perturbed_data_normalized = transforms.Normalize((0.1307,), (0.3081,))(perturbed_data)
# もう一度予測
output = model(perturbed_data_normalized)
final_pred = output.max(1, keepdim=True)[1] # 10クラスの中で最大の確率のindexを取得
# 予測結果が正しい場合
if final_pred.item() == target.item():
correct += 1 # カウント
# イプシロンが0の場合(attackしない場合)
if epsilon == 0 and len(adv_examples) < 5:
adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex) )
# 正しくない場合
else:
# adv examplesを可視化するために、リストに格納
if len(adv_examples) < 5:
adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex) )
# 全てのデータセットに対して処理が完了したら、精度を計算
final_acc = correct/float(len(test_loader))
print(f"Epsilon: {epsilon}\tTest Accuracy = {correct} / {len(test_loader)} = {final_acc}")
# 精度とadv_examplesを返り値とする
return final_acc, adv_examples
accuracies = []
examples = []
# 各イプシロンにおいてtest関数を実行
for eps in epsilons:
acc, ex = test(model, device, test_loader, eps)
accuracies.append(acc)
examples.append(ex)
4. Result
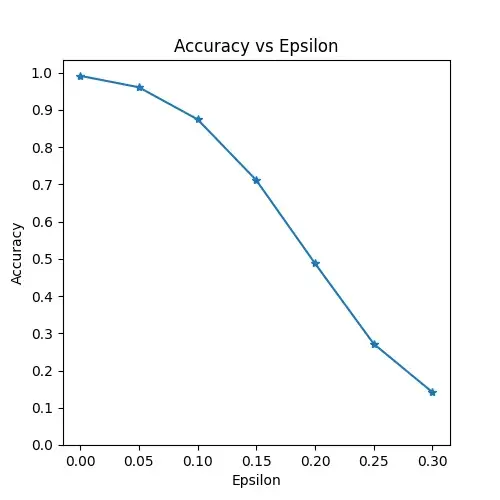
精度とイプシロンの関係をプロットします。イプシロンを大きくすると、予測精度が小さくなることが見てわかると思います。これは、イプシロンが大きくなると、損失を最大化する方向に大きく画像を変化させるためになります。また、イプシロンを線形に変化させても、精度は線形に減少することはありません。
plt.figure(figsize=(5,5))
plt.plot(epsilons, accuracies, "*-")
plt.yticks(np.arange(0, 1.1, step=0.1))
plt.xticks(np.arange(0, .35, step=0.05))
plt.title("Accuracy vs Epsilon")
plt.xlabel("Epsilon")
plt.ylabel("Accuracy")
plt.show()
5. Sample Adversarial Examples
イプシロンが大きくなるにつれて予測精度は低下しますが、その分摂動が目に見えるようになります。現実的に考える場合、精度の低下と知覚可能性のトレードオフを十分に考える必要があります。ここで、攻撃が成功した例を示します。
# Plot several examples of adversarial samples at each epsilon
cnt = 0
plt.figure(figsize=(8,10))
for i in range(len(epsilons)):
for j in range(len(examples[i])):
cnt += 1
plt.subplot(len(epsilons),len(examples[0]),cnt)
plt.xticks([], [])
plt.yticks([], [])
if j == 0:
plt.ylabel(f"Eps: {epsilons[i]}", fontsize=14)
orig,adv,ex = examples[i][j]
plt.title(f"{orig} -> {adv}")
plt.imshow(ex, cmap="gray")
plt.tight_layout()
plt.show()

6. Where to go next?
実際、NIPS 2017では、敵対的攻撃と防御の大会が開催され、多くの手法がこの論文で紹介されています。
防御に関する研究は、機械学習モデルを、自然に加えられた摂動(ノイズ)や攻撃として加えられた摂動の両方に対して、より頑健にするというアイデアにも繋がると考えられます。
普段、皆さんはこのような攻撃について考えたことはありますか?
私は、頭の片隅には敵対的攻撃というワードはあったのですが、普段モデルを作成する上で深く考えたことはありませんでした。
ただただ学習データやテストデータに対して予測精度の良いモデルを作るのではなく、このような敵対的攻撃に対しても強いモデルを作ることもこれから意識していこうと思いました。

今西 渉
大阪大学大学院
生命機能研究科 卒業