DCGAN TUTORIAL

DCGAN TUTORIAL
この勉強会では、DCGAN(Deep Convolutional Generative Adversarial Network)をpytorchで実装したいと思います!
1. What is a GAN?
GANとは、Generative Adversarial Networksの略称であり、深層学習モデルにトレーニングデータの分布を学習させ、その同じ分布から新しいデータを生成するためのフレームワークになります。 GANは、lan Goodfellowによって2014年に考案され、「Generative Adversarial Nets」で紹介されました。GANは、GeneratorとDiscriminatorの二つのモデルで構成されています。
- Generator : トレーニング画像に似た「偽物」の画像(限りなく本物に近い画像)を生成
- Discriminator : 画像を見て、それが偽物の画像か、本物の画像か判断
トレーニング中、GeneratorはDiscriminatorを騙すような画像を生成し、DiscriminatorはGeneratorが生成した画像を偽物、訓練画像を本物と判断するように働きます。このゲームの均衡点は、Generatorが限りなく本物のような偽物の画像を生成し、Discriminatorが常に50%の信頼度でGeneratorの出力が本物か偽物かを推測するようになったときになります。
ここで、チュートリアル全体で使用される表記法を定義します。
まず、Discriminatorから始めます。xは画像を表します。D(x)はDiscriminatorであり、D(x)の入力はCHWサイズが3x64x64の画像です。
xがトレーニングデータの場合は、Dの出力は高く、Generatorが生成した画像の場合は、Dの出力が低くなるべきです。このことから、D(x)は2値分類モデルと考えることもできます。
次に、Generatorについてです。zは標準正規分布からサンプリングされた潜在ベクトルになります。G(z)はGeneratorであり、潜在ベクトルzを画像空間にマッピングします。Gの目標は、トレーニングデータが従う分布pdataを推定し、その推定分布pgから偽物の画像を生成できるようにすることになります。
したがって、D(G(z))は、Generatorの出力が本物の画像である確率になります。Goodfellowの論文でDとGは最小最大ゲームを行います。
つまり、Dは本物画像と偽物画像を正しく分類する確率を最大化しようとし、Gは、Dが偽物と予測する確率を最小化しようとします。
理論的には、この最小最大ゲームの解は、pg = pdataであり、Discriminatorは入力が本物の画像か偽物の画像かをランダムに推測することになります。しかし、GANの収束理論は現在も研究されており、実際にはモデルが最適な状態になるまで学習が進むわけではありません。
2. What is a DCGAN?
DCGANは、Radfordらによって「Unsupervised Representation Learning With Deep Convolutional Generative Adversarial Networks」で紹介されました。前節で紹介したオリジナルのGANとの大きな違いは、GeneratorとDiscriminatorのそれぞれに全結合層ではなく、畳み込み層を使用している点になります(画像AIに全結合層とは、時代を感じます。)。
Discriminatorは、strided convolution layersやbatch norm layers、LeakyReLU関数で構成されています。入力は、3x64x64の画像であり、出力は入力が本物である確率(入力画像が本物かどうか)になります。
Generatorは、convolutional-transpose layersやbatch norm layers、ReLU関数で構成されています。入力は標準正規分布からサンプルされる潜在ベクトルzであり、出力は3x64x64のRGB画像になります(StyleGANを使う私たちからするとかなり小さい、、、)。
convolutional-transpose layersによって、潜在ベクトルを変形し、画像と同じ形状にします。
import argparse
import os
import random
import torch
import torch.nn as nn
import torch.nn.parallel
import torch.optim as optim
import torch.utils.data
import torchvision.datasets as datasets
import torchvision.transforms as transforms
import torchvision.utils as vutils
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML
# 再現性のため、seedを固定
manualSeed = 999
#manualSeed = random.randint(1, 10000) # もし新たな結果が知りたい場合はこちらを使用
print("Random Seed: ", manualSeed)
random.seed(manualSeed) # 組み込みのseed
torch.manual_seed(manualSeed) # pytorchのseed
# 再現性のある結果を得るために必要(同じ入力が与えられ、同じソフトウェア、ハードウェアで実行された場合、常に同じ出力を生成)
torch.use_deterministic_algorithms(True)
3. Inputs
dataloader:データセットフォルダへのパス。workers:DataLoaderでデータを読み込むために使用する。並列実行数。指定することで処理の高速化が期待できる。batch_size:トレーニングで使用するバッチサイズ。DCGANの論文では、128を使用。image_size:トレーニングで使用する画像サイズ。デフォルトは64x64。nc:入力画像のカラーチャネルの数。nz:潜在ベクトルのサイズ。ngf:Generatorを通して伝播された特徴マップの深さと関連。ndf:Discriminatorを通して伝播された特徴マップの深さを設定。num_epochs:トレーニングにおけるエポック数。lr:学習率。DCGANの論文では、0.0002。beta1:Adamのハイパーパラメーター(Adamについてはこちら)。論文では0.5。ngpu:GPUの数。0の場合、CPUを使用。
# データセットのrootディレクトリ
dataroot = "data/celeba"
# dataloaderのworkerの数
workers = 2
# トレーニング中のbatch size
batch_size = 128
# 画像サイズ
image_size = 64
# RGB画像を使用するので、3を指定
nc = 3
# 潜在ベクトルzのサイズ(i.e. generatorの入力サイズ)
nz = 100
# generatorの特徴マップのサイズ
ngf = 64
# discriminatorの特徴マップのサイズ
ndf = 64
# トレーニングのエポック数
num_epochs = 5
# 学習率
lr = 0.0002
# Adamのハイパーパラメーターであるbeta1
beta1 = 0.5
# 使用するGPU数
ngpu = 1
4. Data
この勉強会では、Celeb-A Faces datasetを使用します。このデータセットは、img_align_celeba.zipといった名前でダウンロードされます。
ダウンロードが完了したら、celebaという名前のディレクトリを用意し、そのディレクトリでzipファイルを解凍します。
ディレクトリ構造は以下のようになります。
/path/to/celeba
-> img_align_celeba
-> 188242.jpg
-> 173822.jpg
-> 284702.jpg
-> 537394.jpg
...
これは、ImageFolderを使用するために重要なステップとなっています。ImageFolderを使うためには、データセットのルートフォルダの下にサブディレクトリがある必要があります。
それでは、datasetを作成、dataloaderを作成、そして、実行するためにデバイスを設定します。最終的にトレーニングデータの一部を可視化します。
# datasetの作成。ImageFolderではトレーニングデータのpathを指定することで勝手にdatasetを作成してくれる。transformもこの段階で指定。
dataset = datasets.ImageFolder(root=dataroot,
transform=transforms.Compose([
transforms.Resize(image_size),
transforms.CenterCrop(image_size),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
]))
# dataloderの作成
dataloader = torch.utils.data.DataLoader(dataset, batch_size=batch_size, shuffle=True, num_workers=workers)
device = torch.device("cuda:0" if (torch.cuda.is_available() and ngpu > 0) else "cpu")
real_batch = next(iter(dataloder))
plt.figure(figsize=(8, 8))
plt.axis("off")
plt.title("Training Images")
plt.imshow(np.transpose(vutils.make_grid(real_batch[0].to(device)[:64], padding=2, normalize=True).cpu(), (1, 2, 0)))

transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))を使う理由…
transforms.ToTensor()によって、画像は[0, 1]のレンジで調整されます。
この画像を、平均0.5、標準偏差0.5によって標準化することで、[-1, 1]のレンジに調整することができます。
x' = (x - mean) / std
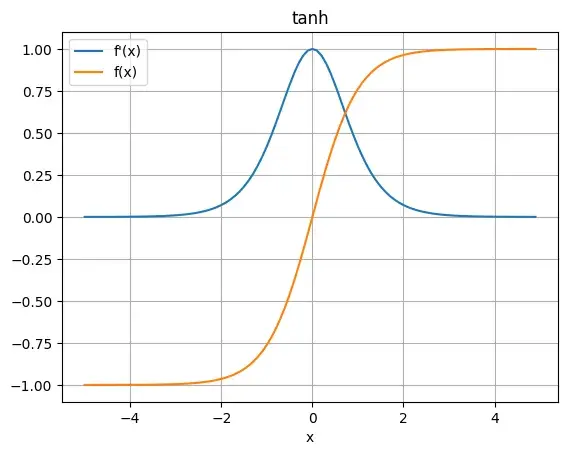
この標準化によって、Generatorの最終活性化関数にtanh関数を採用することができます。tanh関数を適用することで出力のレンジを[-1, 1]に調整することができます。
tanh関数を使用するメリットは、sigmoid関数と比べて、導関数の最大値が1.0と大きいため、学習が進みやすい傾向があります。
5. Weight Initialization
DCGANの論文では、すべてのモデルの重みは、平均0、標準偏差0.02の正規分布からランダムに初期化するのが良いと述べられています。
weights_init関数は初期化されたモデルを入力として受け取り、初期化します。この関数は、モデルの初期化直後に適用されます。
# 重みの初期化関数
def weights_init(m):
classname = m.__class__.__name__
if classname.find('Conv') != -1:
nn.init.normal_(m.weight.data, 0.0, 0.02)
elif classname.find('BatchNorm') != -1:
nn.init.normal_(m.weight.data, 1.0, 0.02)
nn.init.constant_(m.bias.data, 0)
weights_init関数を深掘り!
この初期化関数は、model.apply(weights_init)というような形で使用します。model.apply()を用いることで、モデルの中にある全てのモジュールを再起的に掘って関数を適用することができます。
例えば、あるmodelがConv2dとBatchNorm2dで構成されている場合、model.conv -> model.batchnormと呼び出され、weights_init関数に渡されます。
そのクラス名を取得し、'Conv'や'BatchNorm'が含まれている場合、戻り値は-1以外になるので、初期化する関数が実行されます。
find関数は、文字列の中に特定の文字が含まれているかどうかを探索し、含まれている場合、その特定の文字がスタートするインデックスを返します。
6. Generator
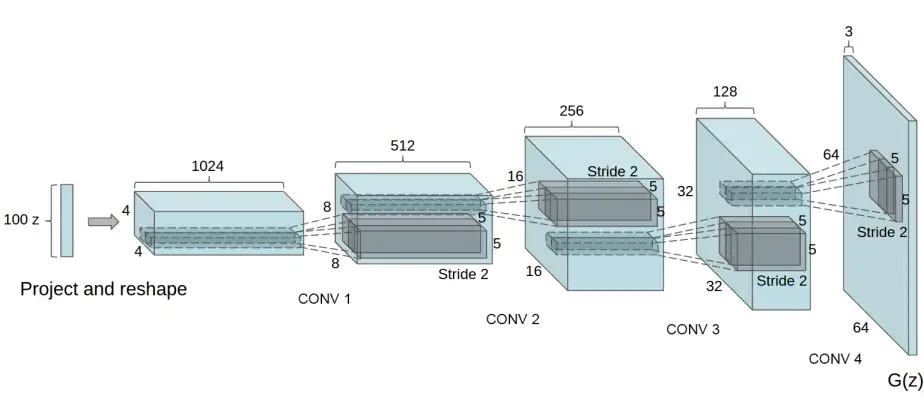
Generatorは、潜在ベクトルを画像空間にマッピングするように学習します。つまり、潜在ベクトルからRGB画像を生成することになります。
実際には、2次元の転置畳み込み層の連続によって実現されます。各層は、2次元のBatch NormalizationとReLU関数とペアになっています。
Generatorの出力はtanh関数によって、入力データの範囲[-1, 1]に戻されます。
転置畳み込み層の後に、Batch Normalizationがあることはかなり重要で、トレーニング中に勾配の流れを助ける役割があります。
# Generator code
class Generator(nn.Module):
def __init__(self, nz, ngf, nc, ngpu):
super().__init__()
self.ngpu = ngpu
self.main = nn.Sequential(
# 入力はZ
nn.ConvTranspose2d(nz, ngf * 8, 4, 1, 0, bias=False),
nn.BatchNorm2d(ngf * 8),
nn.ReLU(True),
# state size. ``(ngf*8) x 4 x 4``
nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
nn.BatchNorm2d(ngf * 4),
nn.ReLU(True),
# state size. ``(ngf*4) x 8 x 8``
nn.ConvTranspose2d( ngf * 4, ngf * 2, 4, 2, 1, bias=False),
nn.BatchNorm2d(ngf * 2),
nn.ReLU(True),
# state size. ``(ngf*2) x 16 x 16``
nn.ConvTranspose2d( ngf * 2, ngf, 4, 2, 1, bias=False),
nn.BatchNorm2d(ngf),
nn.ReLU(True),
# state size. ``(ngf) x 32 x 32``
nn.ConvTranspose2d( ngf, nc, 4, 2, 1, bias=False),
nn.Tanh()
# state size. ``(nc) x 64 x 64``
)
def forward(self, input):
return self.main(input)
Generatorをインスタンス化し、weights_init関数を適用します。
# Generatorをインスタンス化
netG = Generator(nz, ngf, nc, ngpu).to(device)
# multi-GPUで計算する場合
if (device.type == 'cuda') and (ngpu > 1):
netG = nn.DataParallel(netG, list(range(ngpu)))
# weights_init関数を適用して、重みを初期化
netG.apply(weights_init)
# print the model
print(netG)
なぜBatchNorm2dを用いることが学習において有効なのか??
DeepLearningでは、層を重ねることによってモデルを作成します。当然ですが、その場合、一層目の出力が二層目の入力になります。そこで、一層目が学習によってパラメータが変化した場合、二層目への入力の分布が変化することになります。
このように入力の分布が変化してしまうと、学習が不安定になってしまうことがあります。そこでBatchNormを使用することで、ミニバッチごとの統計量を使って、ミニバッチごとに正規化します。
具体的には、ミニバッチごとに平均・分散を計算し、標準化します。その後、γとβによって分布を変化させます。
x' = (x - mean) / std
y = γx' + β
なぜ、標準化した後にバイアスを足し、スケーリングするのか、気になりますよね。単なる標準化だと、平均が0の分布に近づきます。その場合、非線形性を取り入れるために使用している活性化関数が意味のないものになってしまうかもしれません。
というのも、sigmoid関数を想像してもらうとわかりやすいのですが、-1から1の範囲はほぼ線形の部分になります。少しずれた範囲だと、非線形性が増すのでそのような処理を挟むのが良いような気がします。
ここからは、メリットのお話。BatchNormを使用することで、大きな学習率を使用することができます。学習率が大きいと、パラメータの変動が大きくなります。そのため、パラメータが大きくなる場合があり、それが原因で勾配爆発が生じる可能性があります。
しかし、BatchNormを適用することで、勾配が特に変化することはなく、安定につながります(詳しくはこちら)。
また、正則化の効果もあります。BatchNormは毎回違うバッチごとの平均・分散で標準化します。そのため、トレーニングデータが同じものでも毎回少しずつ異なる入力になります。これがノイズとなり、ネットワークを汎化させる正則化の効果があると考えられます。
ConvTranspose2dとは??
特殊な畳み込みで画像サイズを拡大する処理になります。大まかな動作は以下のようになります。
- 入力画像のピクセル間に指定したストライドやパディングの値に応じて数値(0)を埋めて、処理用画像を作成します。
- 処理用画像に畳み込み演算を適用することで出力画像を適用します。
ReLU関数をおさらい!!
ReLU関数は、入力値が正であればそのまま出力し、負であれば0を返す関数になります。
また、導関数の最大値が1.0であるため、勾配消失を改善することができます。また、正の領域は恒等関数であるため計算が簡単で高速化を狙うことができます。しかし、負の値を取る場合、値が0となってしまうため、学習の妨げになる可能性もあります。

7. Discriminator
Discriminatorは、画像を入力として受け取り、入力画像が本物である確率を出力する2値分類モデルになります。
Discriminatorは、3x64x64の画像を受け取り、Conv2d、BatchNorm2d、およびLeakyReLUを通して処理し、最終的な確立をsigmoid関数を介して出力します。
DCGANの論文では、ダウンサンプリングにはプーリングの代わりにstrided convolutionを使用することが効果的であり、これによりネットワークが独自のプーリング関数を学習することができます。
また、Batch NormalizationとLeakyReLU関数は、GとDの学習プロセスにおいて良い勾配の流れをもたらします。
# Discriminator code
class Discriminator(nn.Module):
def __init__(self, ndf, nc, ngpu):
super().__init__()
self.ngpu = ngpu
self.main = nn.Sequential(
# input is ``(nc) x 64 x 64``
nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),
nn.LeakyReLU(0.2, inplace=True),
# state size. ``(ndf) x 32 x 32``
nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
nn.BatchNorm2d(ndf * 2),
nn.LeakyReLU(0.2, inplace=True),
# state size. ``(ndf*2) x 16 x 16``
nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
nn.BatchNorm2d(ndf * 4),
nn.LeakyReLU(0.2, inplace=True),
# state size. ``(ndf*4) x 8 x 8``
nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
nn.BatchNorm2d(ndf * 8),
nn.LeakyReLU(0.2, inplace=True),
# state size. ``(ndf*8) x 4 x 4``
nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
nn.Sigmoid()
)
def forward(self, input):
return self.main(input)
Discriminatorをインスタンス化し、weights_init関数を適用します。
# Discriminatorをインスタンス化
netD = Discriminator(ndf, nc, ngpu).to(device)
# multi-GPUで計算する場合
if (device.type == 'cuda') and (ngpu > 1):
netD = nn.DataParallel(netD, list(range(ngpu)))
# weights_init関数を適用して、重みを初期化
netD.apply(weights_init)
# Print the model
print(netD)
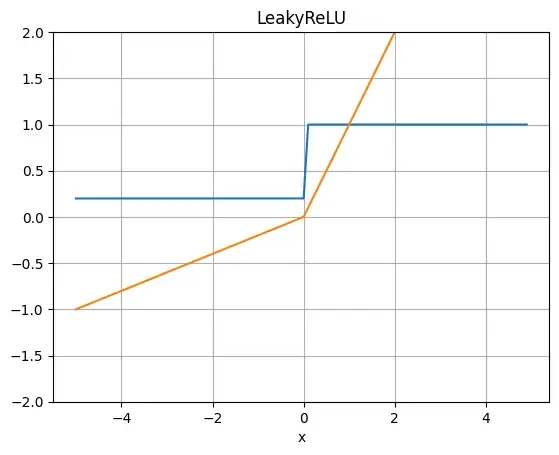
なぜDiscriminatorではLeakyReLU関数を使うのか?
LeakyReLU関数は、入力が正の場合はそのまま出力し、負の場合はある定数をかけて出力します。これにより、勾配が0になって学習が滞るということを防ぐことができます。Generatorを学習する際、Discriminatorを使用するので、Discriminatorで勾配が滞ってしまうとGeneratorが十分に学習することができません。そのため、DiscriminatorではLeakyReLU関数を使用しているそうです。
なぜpoolingを使わないのか?
poolingとは、ダウンサンプリングの一種で、max poolingやavg poolingが存在します。これを使うことによって対象物の位置ずれに対して頑健になります。しかし、poolingを行うことによって特徴マップはより抽象的になり、細かい情報が失われてしまいます。GANにおいて、よりリアルな画像を生成したいため、細かい情報を重視しており、poolingを採用していないと考えられます。その代わりに、畳み込みのストライドを大きくすることでダウンサンプリングを図っています。
8. Loss Functions and Optimizers
DとGの学習には、Binary Cross Entropy loss(BCELoss)を使用します。
Binary Cross Entropy lossは以下のような式で表されます。
l(x,y) = L = {l1, ..., lN}T,
ln = - [yn・logxn + (1 - yn)・log(1 - xn)]
これは、yによって計算する部分が変化します。例えば、y=1の場合、第一項の対数のみ計算し、y=0の場合、第二項の対数のみ計算します。
次に、本物画像のラベルを1、偽物画像のラベルを0と定義します。これらのラベルはDとGの損失の計算時に使用されます。
最後に、DとGの二つに異なるoptimizerを設定します。DCGANの論文で紹介されているように、lr=0.0002とBeta1=0.5のAdamを使用します。
また、Generatorの学習の進行状況を追跡するために、固定された潜在ベクトルをガウス分布から生成します。トレーニングループでは、定期的にこの潜在ベクトルをGに入力し、ノイズから画像が生成されていく過程を観察します。
# BCELossを定義
criterion = nn.BCELoss()
# generatorの進捗を確認するために、固定の潜在ベクトルを生成
fixed_noise = torch.randn(64, nz, 1, 1, device=device)
# トレーニング中のラベルを設定
real_label = 1.
fake_label = 0.
# Adam optimizerを設定
optimizerD = optim.Adam(netD.parameters(), lr=lr, betas=(beta1, 0.999))
optimizerG = optim.Adam(netG.parameters(), lr=lr, betas=(beta1, 0.999))
9. Training
すべての準備が整ったので、トレーニングに移っていきたいと思います。GANの学習は、誤ったハイパーパラメータ設定がモード崩壊を引き起こし、何が間違っているのかがほとんど説明することができないことがあります。ここでは、Goodfellowの論文のAlgorithm1に従いながら、ganhacksで示されたいくつかのベストプラクティスに従います。
具体的には、本物と偽物の画像の異なるミニバッチを作成し、またGの目的関数を調整してlog(D(G(z)))を最大化します。
トレーニングプロセスは、Discriminatorを更新する部分と、Generatorを更新する部分の二つに分けられます。
Part 1 - Train the Discriminator
Discriminatorの学習の目標は、与えられた入力を正確に本物かどうかを分類する確立を最大化することになります。Goodfellowの論文では、「確立的勾配を上昇させることでDiscriminatorを更新する」と述べられています。
実際には、log(D(x)) + log(1 - D(G(z)))を最大化したいと考えています。ganhacksの提案に従い、これを二つのステップで計算します。
まず、トレーニングデータから実画像をサンプルしバッチを作成します。このバッチをDに入力し、損失値log(D(x))を計算します。その後、逆伝播させることで勾配を計算します。
次に、その時点でのGeneratorで偽物画像を生成しバッチを作成します。このバッチをDに入力し、損失値log(1 - D(G(z)))を計算し、逆伝播させることで勾配を蓄積します。
このように実画像と生成画像の両方によって蓄積した勾配を使って、Discriminatorを更新します。
Part 2 - Train the Generator
Generatorの学習では、本物に限りなく近い偽物画像を生成するために、log(1 - D(G(z)))を最小化することを目指します。しかし、学習の初期段階では、十分な勾配がえられないことがGoodfellowによって示されています。
そのため、log(D(G(z)))を最大化するように変更します。つまり、偽物画像のラベルを1としてGの損失関数を計算します。
こうすることで、BCELossの第一項を使用することができ、log(D(G(z)))を計算することになります。
Loss_D:Discriminatorの損失値。log(D(x)) + log(1 - D(G(z)))によって計算された損失値の合計。Loss_G:Generatorの損失値。log(D(G(z)))D(x):すべての実画像におけるDiscriminatorの平均出力。1に近い値から始まり、Gが良くなることで、0.5に近づくことが理想である。D(G(z)):すべての生成画像におけるDiscriminatorの平均出力。0に近い値から始まり、Gが良くなることで、0.5に近づくことが理想である。
# Training Loop
# 学習の進捗を確認するために使用するリスト
img_list = []
G_losses = []
D_losses = []
iters = 0
print("Starting Training Loop...")
# 各epochの処理
for epoch in range(num_epochs):
# 各batchの処理
for i, data in enumerate(dataloder, 0):
'''(1) Discriminatorの更新: log(D(x)) + log(1 - D(G(z)))の最大化'''
# 入力が実画像の場合
netD.zero_grad()
real_cpu = data[0].to(device)
b_size = real_cpu.size(0)
label = torch.full((b_size,), real_label, dtype=torch.float, device=device) # batch_size分の1の配列
output = netD(real_cpu).view(-1) # output_shape: (batch_size, 1, 1, 1)であるため、view(-1)により、(batch_size, )に変形
errD_real = criterion(output, label)
errD_real.backward() # 勾配計算
D_x = output.mean().item()
# 入力が生成画像の場合
noise = torch.randn(b_size, nz, 1, 1, device=device) # Generatorに入力する潜在ベクトル
fake = netG(noise)
label.fill_(fake_label) # batch_size分の0の配列
output = netD(fake.detach()).view(-1) # detachすることで、生成画像までの計算グラフを切り離すイメージ(Generatorの勾配は考慮しない)
errD_fake = criterion(output, label)
errD_fake.backward()
D_G_z1 = output.mean().item()
errD = errD_real + errD_fake
optimizerD.step()
'''(2) Generatorの更新:log(D(G(z)))の最大化'''
netG.zero_grad()
label.fill_(real_label) # batch_size分の1の配列
output = netD(fake).view(-1) # detachせず、Generatorの勾配を考慮する
errG = criterion(output, label)
errG.backward()
D_G_z2 = output.mean().item()
optimizerG.step()
# トレーニング状況を出力
if i % 50 == 0:
print('[%d/%d][%d/%d]\tLoss_D: %.4f\tLoss_G: %.4f\tD(x): %.4f\tD(G(z)): %.4f / %.4f'
% (epoch, num_epochs, i, len(dataloader),
errD.item(), errG.item(), D_x, D_G_z1, D_G_z2))
# plotするために損失値を保存
G_losses.append(errG.item())
D_losses.append(errD.item())
# 固定された潜在ベクトルを用いてGeneratorの状態を確認
if (iters % 500 == 0) or ((epoch == num_epochs-1) and (i == len(dataloader)-1)):
with torch.no_grad():
fake = netG(fixed_noise).detach().cpu()
img_list.append(vutils.make_grid(fake, padding=2, normalize=True))
iters += 1
10. Results
最後に結果を見ていきましょう!
まず、DとGの損失値がどのように変化したかを確認します。次に、各エポック毎に固定された潜在ベクトルに対するGの出力を可視化します。
そして最後に、実画像と生成画像を並べて比較します。
Loss versus training iteration
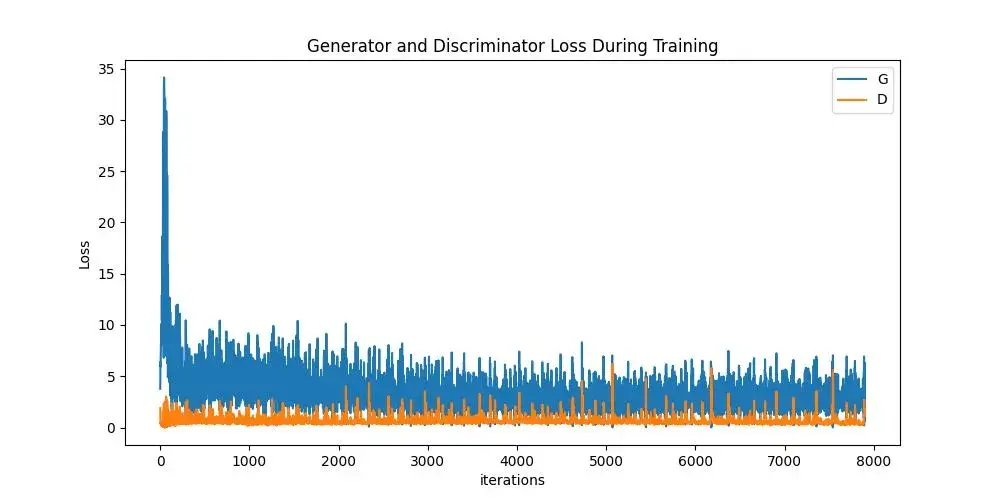
Visualization of G's progression


