Reinforcement Learning (DQN) Tutorial

このチュートリアルでは、Pytorchを用いてDeep Q Learning (DQN)の学習を行います。 タスクとしては、カートに取り付けられたポールが真っ直ぐに保たれるように、カートを左右に動かすというものになります。

CartPole

エージェントは現在の環境の状態を観察し、アクションを選択します。これにより、環境は新しい状態に遷移し、さらにアクションの結果を示す報酬を返します。 今回の場合では、各タイプステップごとの報酬は+1であり、ポールが大きく倒れるか、もしくは、カートが中心から2.4ユニット以上移動すると環境が終了します。 つまり、理想的なシナリオは、より長い期間実行され、より大きな報酬を累積することになります。

CartPoleのタスクは、エージェントへの入力として環境の状態（位置や速度など）を表す4つの実数値を使用するように設計されています。 これらの4つの入力はスケーリングなしで取得し、2つの値（各アクション（右か左）に対して一つずつ）を出力する小さなfully-connected networkに渡します。 このネットワークは、入力状態が与えられた場合に、各アクションにおける期待値を予測するように訓練されます。また、期待値が最も高いアクションが選択されます。

Packages

まず必要なパッケージをインポートします。まず最初に、OpenAI Gymのgymnasiumが必要になります。

pip3 install gymnasium[classic_control]
            

また、Pytorchから以下のものを使用します。

• neural networks（torch.nn）
• optimization（torch.optim）
• automatic differentiation（torch.autograd）

import gymnasium
import math
import random
import matplotlib
import matplotlib.pyplot as plt
from collections import namedtuple, deque
from itertools import count

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F

env = gym.make("CartPole-v1")

# set up matplotlib（ipynbで使用する際に必要となる）
is_ipython = 'inline' in matplotlib.get_backend()
if is_ipython:
    from IPython import display # ipynbで簡単に画像や動画などを表示することができる

# インタラクティブモードをオンにすることでリアルタイム更新が可能（こちらを参考）
plt.ion()

# if GPU is to be used
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
            

Replay Memory

DQNのトレーニングには、experience replay memoryを使用します。experience replay memoryは、エージェントが観測した遷移を保存し、後でこのデータを再利用することができます。 ランダムにサンプリングすることで、バッチを構成する遷移が無相関になります。これにより、DQNのトレーニングが大幅に安定し、改善されることが示されています。

• Transition：環境内の単一の遷移を表すnamedtupleになります。基本的に(state, action)のペアをその(next_state, reward)の結果にマッピングします。
• ReplayMemory：有界サイズの循環バッファであり、直近で観測された繊維を保持します。また、トレーニングのために、ランダムなバッチの遷移を選択するための.sample()も実装しています。

Transition = namedtuple('Transition', 
                        ('state', 'action', 'next_state', 'reward'))
class ReplayMemory(object):

    def __init__(self, capacity):
        self.memory = deque([], maxlen=capacity)

    def push(self, *args):
        self.memory.append(Transition(*args))

    def sample(self, batch_size):
        return random.sample(self.memory, batch_size)

    def __len__(self):
        return len(self.memory)
            

from collections import namedtuple

Vegetable = namedtuple('Vegetable', ('name', 'color'))
best_veggie = Vegetable('生姜', '黄色')
print(f'私の好きな野菜は{best_veggie.name}です。')
# -> 私の好きな野菜は生姜です。

print(f'{best_veggie.name}の色は{best_veggie.color}です。')
# -> 生姜の色は黄色です。
                    

from collections import deque
d = deque(['B', 'C', 'D'])
d.append('E')
print(d)
# -> deque(['B', 'C', 'D', 'E'])

d.appendleft('A')
print(d)
# -> deque(['A', 'B', 'C', 'D', 'E'])

# 最大長を設定
d = deque([1, 2, 3, 4, 5], maxlen=5)
d.append(1)
print(d)
# -> deque([2, 3, 4, 5, 1])

# listの場合
a = list(range(2000))
start = time.time()
for i in range(2000):
    a.pop(0)
end = time.time()
print(end - start)
# -> 0.0008296966552734375

# dequeの場合
b = deque(list(range(2000)))
start = time.time()
for i in range(2000):
  b.popleft()
end = time.time()
print(end - start)
# -> 0.0005195140838623047
            

DQN algorithm

最終ゴールは、一定の割合で減衰した累積報酬 を最大化しようとするpolicyを訓練することになります。 はリターンとも呼ばれます。 減衰率$\mathrm{\gamma }$は$0$から$1$の間の値を取り、和が収束することを保証します。
小さな$\mathrm{\gamma }$は、不確かな遠く離れた未来から得られた報酬をそこまで重要視しない確信度の高い近い未来を重要視する）ことを意味します。 また、agentは、時間的に遠い未来の同等の報酬よりも、時間的に近い報酬を集めるようになります。

Q-learningのメインアイデアは、
もし我々が与えられた状態で行動を取った場合のリターンを教えてくれる関数 $Q^{*}$: $\mathrm{State}\times \mathrm{Action}\mathrm{\to }\mathrm{R}$ があれば、我々の報酬を最大化するpolicyを簡単に構築できるということになります。

${\pi }^{*}\mathrm{(s)}=\underset{a}{\overset{}{\mathrm{argmax}}}{Q}^{*}\mathrm{(s,\; a)}$

しかし、私たちは世界についてすべてわかるわけではなく、$Q^{*}$にアクセスできません。 そこで、普遍的な関数近似であるニューラルネットワークを用いることで、$Q^{*}$を近似することができます。
ここで用いるトレーニングの更新ルールにおいて、すべての$\mathrm{Q}$関数はベルマン方程式に従います。

$Q^{\pi }\mathrm{(s,\; a)}=\mathrm{r}+\mathrm{\gamma }{Q}^{\pi }\mathrm{(s\text{'},\; \pi (s\text{'}))}$

等号の両辺の差は、時間差誤差として知られています。

$\mathrm{\delta }=\mathrm{Q(s,\; a)}-\mathrm{(r}+\mathrm{\gamma <munderover><mi>max</mi><mrow><mi>a</mi></mrow><mi>\text{'}</mi></munderover>Q(s\text{'},\; a))}$

この誤差を最小化するために、Huber損失を使用します。Hubeer損失は、誤差が小さいときは平均二乗誤差のように働き、誤差が大きいときは平均絶対誤差のように働きます。 $\mathrm{Q}$の推定値が非常にノイジーな場合、外れ値に対してよりロバストになります。Huber損失を遷移のバッチで計算し、$\mathrm{B}$はreplay memoryからサンプルされます。

$\mathrm{L}=\frac{1}{\mathrm{|B|}}\sum _{\mathrm{(s,\; a,\; s\text{'},\; r)\in B}}^{}\mathrm{L(\delta )}$

where $\mathrm{L(\delta )}=\{\begin{array}{c}\frac{1}{2}{\delta }^{\mathrm{<mn>2</mn>}}& \mathrm{for\; |\delta |\; \le \; 1}\\ \mathrm{|\delta |}-\frac{1}{2}& \mathrm{otherwise}\end{array}$

Q-network

今回使用するモデルは、現在のスクリーンパッチと以前のスクリーンパッチの差を取り込むフィードフォワードニューラルネットワークになります。 また、そのネットワークは、$\mathrm{Q(s,\; left)}$と$\mathrm{Q(s,\; right)}$を出力します。ここでの$\mathrm{s}$はネットワークの入力になります。 事実上、このネットワークは、現在の入力が与えられたときに、それぞれの行動を取った場合の期待される収益を予測しようとします。

class DQN(nn.Module):

    def __init__(self, n_observations, n_actions):
        super().__init__()
        self.layer1 = nn.Linear(n_observations, 128)
        self.layer2 = nn.Linear(128, 128)
        self.layer3 = nn.Linear(128, n_actions)
    
    # 次のアクションを決定するために一つの要素で呼び出されるか、
    # 最適化中に一括で呼び出されるか
    def forward(self, x):
        x = F.relu(self.layer1(x))
        x = F.relu(self.layer2(x))
        return self.layer3(x)

            

Training

Hyperparameters and utilities

ここでは、modelとoptimizerをインスタンス化し、いくつかのユーティリティを定義します。

• select_action：$\mathrm{\epsilon }$-greedy policyに従ってアクションを選択します。簡単に言えば、アクションの選択にモデルを使うこともあれば、一様にサンプリングすることもあります。ランダムなアクションを選択する確率はEPS_STARTから始まり、EPS_ENDに向かって指数関数的に減衰します。EPS_DECAYは減衰の速度をコントロールします。
• plot_durations：エピソードの持続時間をプロットするヘルパーで、直近の100エピソードの平均を表示します。このプロットはメインのトレーニンググループを含むセルの下に表示され、各エピソードの後に更新されます。

BATCH_SIZE = 128    # BATCH_SIZE : replay bufferからサンプルされる遷移の数
GAMMA = 0.99        # GAMMA : 減衰率
EPS_START = 0.9     # EPS_START : epsilonの初期値
EPS_END = 0.05      # EPS_END : epsilonの最終的な値
EPS_DECAY = 1000    # EPS_DECAY : epsilonの指数関数的減衰の割合を制御。高い値の場合、ゆっくりと減衰される。
TAU = 0.005         # TAU : ネットワークの更新率
LR = 1e-4           # LR : 学習率

# gym action spaceからアクション数を取得
n_actions = env.action_space.n

# 状態観測の回数を取得
state, info = env.reset()
n_observations = len(state)

policy_net = DQN(n_observations, n_actions).to(device)
target_net = DQN(n_observations, n_actions).to(device)
target_net.load_state_dict(policy_net.state_dict())

optimizer = optim.AdamW(policy_net.parameters(), lr=LR, amsgrad=True)
memory = ReplayMemory(10000)

steps_done = 0

def select_action(state):
    global steps_done # グローバル変数とすることで関数外でもこの値が参照される
    sample = random.random() # 0.0以上1.0未満の値を返す
    eps_threshold = EPS_END + (EPS_START - EPS_END) * \
        math.exp(-1. * steps_done / EPS_DECAY)

    steps_done += 1
    if sample > eps_threshold:
        with torch.no_grad():
            # t.max(1)は、各行の最大の列の値を返す
            return policy_net(state).max(1)[1].view(1, 1)
    else:
        return torch.tensor([[env.action_space.sample()]], device=device, dtype=torch.long)

def plot_durations(show_result=Falase):
    plt.figure(1) # unique identifierを1として作成
    durations_t = torch.tensor(episode_durations, dtype=torch.float)
    if show_result:
        plt.title('Result')
    else:
        plt.clf() # 現在のfigureを削除
        plt.title('Training...')
    plt.xlabel('Episode')
    plt.ylabel('Duration')
    plt.plot(durations_t.numpy())
    # 100 episodeの平均を計算し、それらをplot
    if len(durations_t) >= 100:
        means = durations_t.unfold(0, 100, 1).mean(1).view(-1) # dim=0の方向から100個切り出し、平均を計算
        means = torch.cat((torch.zeros(99), means))
        plt.plot(means.numpy())

    plt.pause(0.001) # plotを更新するために一時停止する
    if is_ipython:
        if not show_result:
            display.display(plt.gcf()) # plt.gcf()によって現在のfigureを返す
            display.clear_output(wait=True) # 本ステップが含まれたセルの出力だけを消去（wait=Trueによって、次の出力まで待機）
        else:
            display.display(plt.gcf())
            

Training loop

最後にモデルを学習させます。
ここでは、最適化の単一ステップを実行するoptimize_model関数を定義します。この関数は、まずバッチをサンプリングし、すべてのテンソルを連結することで一つのテンソルにします。 $\mathrm{Q(<msub><mi>s</mi><mi>t</mi></msub>,\; <msub><mi>a</mi><mi>t</mi></msub>)}$と$\mathrm{V(<msub><mi>s</mi><mi>t+1</mi></msub>)}={\max }_a\mathrm{Q(<msub><mi>s</mi><mi>t+1</mi></msub>,\; a)}$を計算し、 それらを組み合わせて損失とします。$\mathrm{s}$が終端状態であれば、$\mathrm{V(s)}=0$となります。 また、安定性を増すために、ターゲットネットワークを用いて$\mathrm{V(<msub><mi>s</mi><mi>t+1</mi></msub>)}$を計算します。 ターゲットネットワークは、ハイパーパラメータTAUによって制御されるsoft updateを用いてマイステップ更新されます。

def optimize_model():
    if len(memory) < BATCH_SIZE:
        return

    transitions = memory.sample(BATCH_SIZE)
    # batchをtransposeする
    # これは、Transitionのバッチ配列をバッチ配列のTransitionに変換する
    batch = Transition(*zip(*transitions))

    # 非最終状態のマスクを計算し、バッチ要素を連結
    # （最終的な状態とは、シミュレーションが終了した後の状態である）
    non_final_mask = torch.tensor(tuple(map(lambda s: s is not None, batch.next_state)), device=device, dtype=torch.bool)
    non_final_next_states = torch.cat([s for s in batch.next_state if s is not None])

    state_batch = torch.cat(batch.state)
    action_batch = torch.cat(batch.action)
    reward_batch = torch.cat(batch.reward)

    # Q(s_t, a)を計算 - モデルがQ(s_t)を計算し、次に取られたアクションの列を選択する
    # これらは、policy_netに従って各バッチ状態に対して取られたであろうアクションである
    state_action_values = policy_net(state_batch).gather(1, action_batch)

    # すべての次の状態においてV(s_{t+1})を計算する
    # non_final_next_statesにおけるアクションの期待値は
    # 古いtarget_netに基づいて計算される
    # マスクに基づいてマージされ、期待される状態の値か、状態が最終的なものであった場合は0が得られる
    next_state_values = torch.zeros(BATCH_SIZE, device=device)
    with torch.no_grad():
        next_state_values[non_final_mask] = target_net(non_final_next_states).max(1)[0]
        # 期待されるQの値を計算
        expected_state_action_values = (next_state_values * GAMMA) + reward_batch

        # Huber損失を計算
        criterion = nn.SmoothL1Loss()
        loss = criterion(state_action_values, expected_state_action_values.unsqueeze(1))

        # モデルを最適化する
        optimizer.zero_grad()
        loss.backward()
        torch.nn.utils.clip_grad_value_(policy_net.parameters(), 100) # 閾値を超えた勾配のみがクリッピングされる（勾配爆発防止）
        optimizer.step()
            

以下にメイントレーニングループを示します。 最初に環境をリセットし、初期状態テンソルを取得します。 次に、アクションをサンプリングし、実行し、次の状態と報酬（常に１）を観察し、モデルを最適化します。 エピソードが終了すると（モデルが失敗すると）ループを再開します。

以下では、GPUが利用可能な場合、num_episodesは600に設定され、そうでない場合は、トレーニングに時間がかかりすぎないように50が設定されます。 しかし、CartPoleで良好なパフォーマンスを観察するには、50エピソードでは不十分です。600のトレーニングエピソード内でモデルが常に500ステップを達成することを確認する必要があります。 RLエージェントのトレーニングはノイズの多いプロセスであるため、収束が観察されない場合、トレーニングを再開するとより良い結果が得られます。

if torch.cuda.is_available():
    num_episodes = 600
else:
    num_episodes = 50

for i_episode in range(num_episodes):
    # 環境をリセットし、状態を取得 
    state, info = env.reset()
    state = torch.tensor(state, dtype=torch.float32, device=device).unsqueeze(0)
    for t in count():
        action = select_action(state)
        observation, reward, terminated, truncated, _ = env.step(action.item())
        reward = torch.tensor([reward], device=device)
        done = terminated or trucated

        if terminated:
            next_state = None
        else:
            next_state = torch.tensor(observation, dtype=torch.float32, device=device).unsqueeze(0)
        
        # memoryにtransitionを保存
        memory.push(state, action, next_state, reward)

        # 次の状態に移行
        state = next_state

        # (policy networkにおいて)最適化ステップを実行
        optimize_model()

        # ターゲットネットワークの重みをSoft update
        # θ' ⇦ τ θ + (1 - τ)θ'
        target_net_state_dict = target_net.state_dict()
        policy_net_state_dict = policy_net.state_dict()
        for key in policy_net_state_dict:
            target_net_state_dict[key] = policy_net_state_dict[key] * TAU + target_net_state_dict[key]*(1-TAU)
        target_net.load_state_dict(target_net_state_dict)

        if done:
            episode_durations.append(t + 1)
            plot_durations()
            break

print('Complete')
plot_durations(show_result=True)
plt.ioff()
plt.show()
            

全体的なデータの流れを示した図はこちらになります。

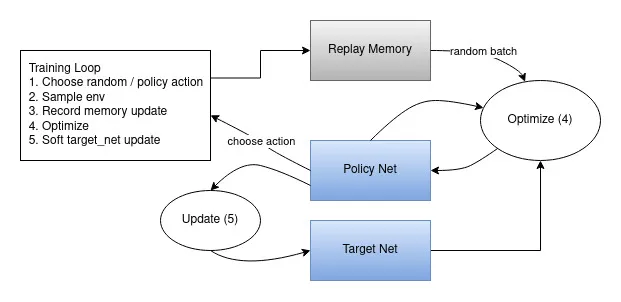
アクションはランダムに、あるいはpolicyに基づいて選択され、gym環境から次のステップのサンプルを取得します。その結果をreplay memoryに記録し、繰返し毎に最適化ステップを実行します。 最適化はreplay memoryからランダムなバッチを選択し、新しいpolicyのトレーニングを行います。古いtarget_netもまた、期待される$\mathrm{Q}$値を計算するために最適化で使用されます。 重みのソフト更新はステップ毎に実行されます。